This is a series about creating mathematical curves in BricsCAD (and AutoCAD).
Part 0, just hackish with a spreadsheet, result driven.
Part 1, the math, understanding ways to iterate.
Part 2, the coding, techniques available.
THIS ARTICLE IS UNDER CONSTRUCTION. YOUR POSITIVE INPUT IS APPRECIATED.
In part 1 the mathematics are explained. It turns out to be a solid base with a very functional algorithm in order to draw approximated curves.
Table of Contents
Status Quo
This pages offers clues for coding. I’ve tried several concepts as described in part 1. After ending up writing a few hundred lines of code I decided to stop because a proper solution is simply a lot of work in unpaid time that lacks.
That is not the complete story, after tinkering, I also came to the conclusion that using a non uniform rational basis spline, or NURBS , or spline is a proper alternative after all and, combined with the theories in part 1, it offers best possibilities (and consumes a lot of my time).
Does it mean that this page is worthless? No, it offers additional insights that you will not find on the net in a structured way.
Making a NURBS
Ways in Lisp
In Lisp there are several ways to create a NURBS or spline:
- Very easy with (command “._spline” …), not recommended for production environments.
- The object-way with (vla-AddSpline …), not discussed further.
- The old fashioned way, using (entmake …), discussed here.
Example
“Entmake” that spline
Consider the following code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | (setq point-list '((0 0) (1 1) (2 0) (3 -2) (4 0))) (entmake (append (list '(0 . "SPLINE") '(100 . "AcDbEntity") '(100 . "AcDbSpline") '(70 . 4) '(71 . 3) (cons 74 (length point-list)) ) (mapcar '(lambda (xy) (cons 11 xy)) point-list) ) ) |
The first line is paste-able on the CAD command line as:
(setq point-list '( (0 0) (1 1) (2 0) (3 -2) (4 0))) |
The second part as:
(entmake (append (list '(0 . "SPLINE") '(100 . "AcDbEntity") '(100 . "AcDbSpline") '(70 . 4) '(71 . 3) (cons 74 (length point-list))) (mapcar '(lambda (xy) (cons 11 xy)) point-list))) |
Going through the code:
- “70 . 4” is DXF code 70 for spline type 4, i.e. “Rational spline”.
- “71 . 3” means degree 3.
- There are 5 points, so: “74 . 5”.
- “(mapcar “(lambda (xy) (cons 11 xy)) point-list)” returns a list with code “11” sublists: “((11 0 0) (11 1 1) (11 2 0) (11 3 -2) (11 4 0))”
That is all it takes to create a spline. Code “11” points are fit-points, going through the curve, what we want. This could also be “10” for control-points.
There is much more to be aware of, see DXF-codes for Splines. and more on NURBS at Wikipedia.
How to feed mathematical functions to the program?
We’ll start with a few examples.
Function files
Let’s say, we have a function ![]() . What we do is put it in a file with extension fun, for example: curve.fun. The filename should represent what you define in the file.
. What we do is put it in a file with extension fun, for example: curve.fun. The filename should represent what you define in the file.
Please, do yourself a favour, use a suitable text editor like notepad++ and mark your code as Lisp during editing.
Syntax explained
What is in the file? First of all: Valid Lisp code, more on that later. What is needed is:
- A safety factor to make sure the curve is within the deviation limits: fuzzy
- A maximum deviation: dev
- A tolerance as a part of dev: tol
- A start value for x: xmin
- An end value for x: xmax
- Divide calculations: xdiv
- The function: fx
A valid file contains:
1 2 3 4 5 6 7 | (tol 0.2) (fuzzy 0.000) (dev 0.05) (xmin 0) (xmax 2) (xdiv 1) (fx (* x x)) |
That should be clear, setq assigns a value to a variable. What can go wrong? The number of opening parenthesis should be equal to the number of closing parenthesis. That is the number 1 error.
Defining your functions
Arithmetic functions
Here is a list of some arithmetic functions…
| (+ [number number] …) | Add |
| (- [number number] …) | Subtract |
| (* [number number] …) | Multiply |
| (/ [number number] …) | Divide |
| (~ int) | Bitwise NOT |
| (1+ number) | Increment |
| (1- number) | Decrement |
| (abs number) | Absolute value |
| (atan num1 [num2] ) | Arctangent of num1 or num1/num2 |
| (cos ang) | Cosine |
| (exp number) | “e” raised to power |
| (expt base power) | Base raised to power |
| (fix number) | Nearest smaller integer |
| (float number) | Number to real |
| (gcd int1 int2) | Greatest common denominator |
| (log number) | Natural log of number |
| (logand int int …) | Logical bitwise AND |
| (logior int int …) | Logical bitwise inclusive OR |
| (lsh int numbers) | Logical bitwise shift by numbers |
| (max number number …) | Largest of numbers |
| (min number number …) | Smallest of numbers |
| (sin ang) | Sine |
| (sqrt number) | Square root |
Examples
- Note that 6 is an integer and 6.0 is a real.
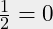
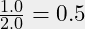 (!)
(!)
- Angles are in radians, 2*pi radians is 360 degrees.
- Expressions are evaluated inside out: (than-this (first-this))
The line containing a function, (fx (* x x)), is a list in a list. The examples below are like (fx (example)).
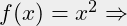 (* x x)
(* x x)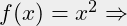 (expt x 2)
(expt x 2)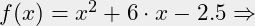 (+ (* x x) (* 6.0 x) -2.5)
(+ (* x x) (* 6.0 x) -2.5)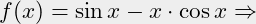 (- (sin x) (* x (cos x)))
(- (sin x) (* x (cos x))) (abs x)
(abs x)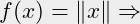 (int x)
(int x)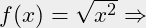 (sqrt (expt x 2))
(sqrt (expt x 2))
How configuration data is handled
What curve does is very basic: It reads lines from the files an interpretes them when they are in list format. A bit more in detail: the line “(xmax 3.2)” is a string. By using the read function, the line is converted to a list. From that point, further processing in Lisp is possible with a set statement (not setq).
Additional considerations
The math part describes a way to calculate valid fit points by iterating checks based on core CAD-Lisp functions. In addition, it is possible to use a set of curve measurement Lisp functions – link broken, cache:
| Function | Description |
|---|---|
| (vlax-curve-getArea curve-obj) | Returns the area inside the curve |
| (vlax-curve-getDistAtParam curve-objparam) | Returns the length of the curve's segment from the curve's beginning to the specified point |
| (vlax-curve-getDistAtPoint curve-objpoint) | Returns the length of the curve's segment between the curve's start point and the specified point |
| (vlax-curve-getEndParam curve-obj) | Returns the parameter of the endpoint of the curve |
| (vlax-curve-getEndPoint curve-obj) | Returns the endpoint (in WCS coordinates) of the curve |
| (vlax-curve-getParamAtPoint curve-objparam) | Returns the distance along the curve from the beginning of the curve to the location of the specified parameter |
| (vlax-curve-getParamAtPoint curve-objpoint) | Returns the parameter of the curve at the point |
| (vlax-curve-getPointAtDist curve-objdist) | Returns the point (in WCS coordinates) along a curve at the distance specified by the user |
| (vlax-curve-getPointAtParam curve-objparam) | Determines the point on the curve that corresponds to the param parameter and returns the point |
| (vlax-curve-getStartParam curve-obj) | Returns the start parameter on the curve |
| (vlax-curve-getStartPoint curve-obj) | Returns the start point (in WCS coordinates) of the curve |
| (vlax-curve-isClosed curve-obj) | Determines if the specified curve is closed (i.e., start point is same as endpoint) |
| (vlax-curve-isPeriodic curve-obj) | Determines if the specified curve has an infinite range in both directions and there is a period value dT, such that there is a point on curve at (u + dT) = point on curve (u), for any parameter u |
| (vlax-curve-isPlanarcurve-obj) | Determines if there is a plane that contains the curve |
| (vlax-curve-getClosestPointTo curve-obj givenPnt [extend]) | Returns the point (in WCS coordinates) on a curve that is nearest to the specified point |
| (vlax-curve-getClosestPointToProjectioncurve-obj givenPnt normal [extend]) | Returns the point (in WCS coordinates) on a curve that is nearest to the specified point |
| (vlax-curve-getFirstDeriv curve-obj param) | Returns the first derivative (in WCS coordinates) of a curve at the specified location |
| (vlax-curve-getSecondDerivcurve-obj param) | Returns the second derivative (in WCS coordinates) of a curve at the specified location |
In BricsCAD these functions are also available on OS-X and Linux.