Er zijn diverse online calculators voor draadberekeningen. Ze werken als een black-box. Je stopt er gegevens in en jouw draadkeuze ligt vast. Dat is allemaal heel leuk en handig maar wie zegt je dat de uitkomsten kloppen? Omdat het relatief eenvoudig is om zo’n berekening met de hand te maken en vooral om beter te begrijpen wat de gevolgen zijn, volgt hier een korte post.
Table of Contents
De gevolgen van de draadkeuze
Voor een verantwoorde keuze spelen diverse zaken een rol. Met name:
- Hoeveel spanningsverlies, door de weerstand van de kabel zelf, is acceptabel? Dat is immers van belang voor:
- De werking van aangesloten apparaten. Denk aan een koelkast die op 12 Volt prima werkt maar bij 11 V simpelweg stopt.
- De warmteontwikkeling in de kabel. Als de kabel te heet wordt dan ontstaat er brandgevaar.
- Economische motieven:
- Het rendement speelt een rol, verwarming van bedrading betekent ook energieverlies. Het betekent de toepassing van zwaardere energiebronnen ter compensatie.
- Andersom is een draad die te zwaar is een verspilling van grondstoffen, terwijl de beperking van spanningsverlies geen rol meer speelt. Bovendien moeten die extra kilo’s koper mee vervoerd worden bij mobiele toepassingen.
- Duurzame motieven: In de automobielsector en apparatenbouw dient de bedrading “goed genoeg” te zijn gedurende de levensduur van een product – in het beste geval. Dat betekent in de regel: tegen minimale kosten produceren. Haaks daarop staat een “Total Cost of Ownersip-berekening”, waarbij het rendabel kan zijn om meer uit te geven aan materiaal en arbeid.
Een voorbeeldberekening
De soortelijke weerstand ![]() van koper ligt in de orde van:
van koper ligt in de orde van:
![]()
Dat is dus de weerstand tussen twee evenwijdige vlakken van een kubus van koper met een volume van ![]() :
:
Vertaald naar een draad van 1 meter lang en 1mm2 doorsnede komt dat overeen met ![]() – er passen immers 1000 * 1000 draden in 1 m2. De weerstand van die draad is
– er passen immers 1000 * 1000 draden in 1 m2. De weerstand van die draad is ![]() . Dat is een vast gegeven.
. Dat is een vast gegeven.
Merk op dat ik liever praat over het oppervlak van de doorsnede dan over de draaddiameter. Dat is een verbastering en strikt de dikte van de draad, niet het oppervlak van de doorsnede. Dus met draaddoorsnede wordt het oppervlak van de aders van een kabel bedoeld.
Het is ook een goed moment om te beseffen dat als je de lengte van de draad verdubbeld, de weerstand ook verdubbeld. Als je de draaddoorsnede verdubbeld dan halveer je de weerstand. Een kabel van 3 meter met een draaddoorsnede van 0.75 mm2 heeft dus de zelfde weerstand als eentje van 6 meter lang en 1.5 mm2 draaddoorsnede.
Je kan een apparaat en de kabel zien als een serieschakeling op een accu van 12 V. Dus bij een Voltageverlies van de kabel van 1% staat er een spanningsverschil – wat je ook kan meten – tussen het begin en het eind van de kabel van 0.12 V. Voor het apparaat blijft dan 11.88 V over – 99%.
Stel dat het totale vermogen van de kring, apparaat en een kabel, 12 Watt is. In dat geval gaat er 1 Ampère door de kring, immers:
![]()
Het gedeelte van het vermogen dat door de draad geconsumeerd wordt is:
![]()
Dat is belangrijk om te bepalen of de draad niet te warm wordt. Daarnaast weten we nu de weerstand:
![]()
We weten ook de weerstand van draad: ![]() . Een draad met een lengte van
. Een draad met een lengte van ![]() is in dat geval toegestaan.
is in dat geval toegestaan.
Praktijk
Voltageverlies
Wat is een acceptabel Voltageverlies? 4% wordt door velen als teveel gezien. Waarden van 2% a 3% zijn blijkbaar acceptabel. Dat is dus 0.24 a 0.36 V. persoonlijk ervaar ik 3% als teveel.
Totale draadlengte
Dat is misschien wat voor de hand liggend maar toch goed om te beseffen: De totale draadlengte bestaat uit de optelsom van de toevoerdraad (plus) en de afvoerdraad (minus). Dus bij een systeem zoals een auto, waarbij het chassis als weerstandsloze minus gezien wordt, moet ook het stuk(je) draad naar het chassis meegenomen worden.
Legeringen
Tor nu toe is uitgegaan van koper, maar aluminium en ijzer worden worden ook gebruikt. Als zuiver element en goed gegloeid hebben deze metalen optimale geleiding. Kleine hoeveelheden vervuiling of legeringselementen kunnen grote invloed hebben. Zo is roestvast staal (ijzer met beperkte toevoegingen van nikkel en chroom) ongeveer 7 keer minder geleidend dan puur ijzer. Koper met een zuiverheid van 99.9%, waarin sporen fosfor zitten (om zuurstof eruit te halen), heeft maar 85% van de geleiding over. Daarom wordt koper elektrolytisch veredeld. Het wil ook niet zeggen dat je Cu99.9 niet moet gebruiken, het is nog steeds een uitstekende geleider. Echter je moet er bij berekeningen wel rekening mee houden.
Wat is er te koop?
Daar waar het Anglo-Saksische systeem als basis de AWG-classificatie heeft, is het in metrische gebieden gelukkig de gewoonte om SI-eenheden te hanteren. Rond draaddoorsneden altijd af naar boven. Veelvoorkomende doorsneden: 0.25 0.5 0.75 1 1.5 2 2.5 4 mm2. Omzetten van metrisch naar AWG en vice versa: Er staan veel tabellen online.
De hoeveelheid aders peelt ook een rol. Het materiaal wordt meer flexibel en breekt minder snel. In mobiele toepassingen is dat een belangrijk aspect en zal je dus nooit installatiedraad zoals in je huis gebruikt tegenkomen – tenzij het van voor tot achter helemaal vast zit.
De formules voor de bepaling van de draaddoorsnede
Voor hoge vermogens
Een inverter van 4200 W heeft 350 A stroom nodig van 12 V. Tussen de inverter en de accu zit 100 cm kabel. De inverter kan kortstondige piekbelastingen van 8400 W verwerken.
Het blijkt lastig om te zijn om hier uniforme informatie over te vinden. Zelf hanteer ik als absolute grenzen 15 A of 180 W per mm2 voor piekbelastingen en 10 A of 120 W per mm2 voor permanente belasting. In het voorbeeld komt dat neer op 47 mm2 tijdens de pieken en 35 mm2 continu. Het wordt dus een kabel van 50 mm2 in eerste instantie. Maar…
Als de piekbelasting door de onderstaande formule gehaald wordt, dan komt daar ook 50 mm2 uit. Dat betekent dat 2% van 8400 W, 170 Watt dus gebruikt wordt voor de opwarming van de kabel van 1 meter.
Die kabel wordt dus af en en toe gewoon behoorlijk heet. Dat is moeilijk te accepteren. Bovendien is 170 W weggooien, in een systeem waar stroom meestal schaars is, gewoon zonde. Dus is het de moeite waard om vooral de afstand van inverter tot accu te verkleinen maar is het ook een idee om de draaddoorsnede te vergroten en of te denken aan vaste geleiders zoals strippen koper of aluminium.
Voor lage vermogens
De formule berekent het oppervlak A van de geleider in mm2. Dus een uitkomst van A = 0.49 mm2 moet dan vertaald worden naar een draad van minimaal 0.5 mm2 waarbij 0.75 mm2 mogelijk verstandiger is.
Variabelen
- Draadlengte l (m)
- Spanningsverliespercentage f (100*Vverlies/Vtotaal)
- Apparaatvermogen P (W)
- SysteemVoltage U (V)
- Soortelijke weerstand
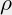 (
(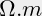 )
)- Koper:
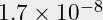
- Messing:

- Aluminium:
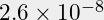
- Constructiestaal:
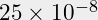
- Koper:
De algemene formule
![]()
Afgeleide formule voor 12 V, koper en 2% verlies
![]()
Voorbeeld: Een LED-strip van 17 W heeft 2.6 m draad nodig plus 10 cm naar de massa (2.7 m totaal dus). De berekening is dan:
![]()
Opmerking 1: Controleer altijd of je zeer ruim onder 10 A of 120 W per mm2 draadstroom zit. Indien dat niet zo is dan is het een verbinding met hoog vermogen, zie hiervoor.
Opmerking 2: Als je de diameter verdubbelt (0.27 mm2 wordt 0.54 mm2) dan halveer je het spanningsverlies (2% wordt dan 1%). Kies je in dit geval 0.5 mm2, dan is het verlies net iets meer dan 1%
Goedendag, in de algemene formule zie ik ook een f voor komen. Waar staat deze f voor, of is dit de berekening voor wisselspanning?
De berekening voor 12V kan/mag ook gebruikt worden voor 24V?
Die f is het geaccepteerde spanningsverlies over de draad. In de afgeleide formule voor 12V is 2% verlies gebruikt.
Dezelfde berekening van draaddoorsnede A in mm², met draadlengte l (m) en vermogen P (Watt) is voor 24 Volt dan:
(rho*10E8*l*P)/(f*U²)=
(1.7*10E⁻8*10E8*l*P)/(2*24*24)=
0.0015*l*P.
Verdubbel je het Voltage (12 > 24), dan heb je een kwart van de draaddoorsnede nodig.
Hallo,
Ik wil 5 led lampen van 12volt gebruiken.
De lampen zijn om de 15 meter van elkaar.
Ik wil telefoon draad gebruiken, is dat goed?
Alvast bedankt.
Dat is afhankelijk van een hoop factoren. Telefoondraad is meestal 0.6 mm2 en als je 5 A/mm2 als maximum neemt kan je dus 0.6 * 5 = 3 A door zo’n draad sturen. Uitgaande van een parallelschakeling van de lampen voedt het eerste stuk draad alle lampen en dan kom je op 0.6 A per lamp uit, keer 12 V is dat een maximum vermogen van 7.2 W per lamp.