Heer Max Verstappen Dendert Over Asfalt

We hebben het over rekenvolgorde, of beter bewerkingsvolgorde, zoals je die geleerd hebt op de middelbare school. “Meneer Van Dalen Wacht Op Antwoord” is uit de gratie en blijkbaar kent letterlijk niemand meer “Heer Van Dalen At Oliebollen” – tot mijn stomme verbazing.

Table of Contents

De huidige lagere school-regel

Tegenwoordig zijn de ezelsbruggetjes:

De eenvoudige: Hoe moeten wij van de onvoldoendes afkomen?
Met een aanwijzing voor gelijkwaardigheid: Hé, Mw. v/d Aorta!

Welnu, meneer van Dalen is dood, lang leve meneer van Dalen! Een kleine wijziging en… (trommelgeroffel…) Dames en heren, ik presenteer aan u enkele alternatieven:

Heer Max Van Dalen At Oliebollen

Heer Max Verstappen Domineert Alle Oliebollen

Heer Max Verstappen Dendert Over Azerbaijan

Heer Max Verstappen Dendert Over Asfalt

De rekenvolgorde is daarbij:

Haakjes
Machtsverheffen
Vermenigvuldigen en of Delen, altijd van links naar rechts
Optellen en of Aftrekken, ongeacht volgorde

Een voorbeeld

$( 2 + 3 ^ 2 ) + 18 / 2 =$
Je start met wat tussen haakjes staat. Machtsverheffen eerst levert op: $( 2 + 9 ) + 18 / 2 =$
Dan tel je op wat tussen haakjes staat: $11 + 18 / 2 =$
Eerst delen: $11 + 9 =$
Dan optellen en dan krijg je: $20$

Het lijkt allemaal makkelijk, maar viraal op het internet was deze som:

$8 \div 2 ( 2 + 2 )$

“Heer Max Van Dalen At Oliebollen” en uitvoeren van links naar rechts levert het enige juiste antwoord op:

De uitdaging anders geschreven: $8 / 2 * ( 2 + 2 ) =$
Eerst wat tussen haakjes staat en je krijgt: $8 / 2 * 4 =$
Vermenigvuldigen of delen, het maakt niet uit welke van die twee want er is geen rangorde, maar wel altijd van links naar rechts, dus eerst $8 / 2$ uitrekenen. Dit levert dan deze som op: $4 * 4 =$
Het antwoord is dus: $16$

Als het principe van “links naar rechts” niet goed gebruikt wordt dan gaat het fout:

$8 \div 2 ( 2 + 2 ) =$
Weer eerst de haakjes: $8 / 2 * 4 =$
Beginnen met 2*4 is niet van links naar rechts voor delen en of vermenigvuldigen: $8 \div 8 =$
En dus is het antwoord $1$ gewoon fout!

Intermezzo worteltrekken
In het rijtje hierboven mis je waarschijnlijk “worteltrekken”. Even een opfrissertje: 2*2, dus “twee in het kwadraat”, levert 4 op. Notatie rekenblad: 2*2 (“twee keer twee”) of 2^2 (“twee tot de macht twee”). Notatie wiskunde: $2 ^ 2$ . Dan is er nog dat vaak vergeten regeltje:
“Worteltrekken is machtsverheffen met het omgekeerde.”
Verduidelijkt met een voorbeeld: “Twee tot de macht vier”, of 2^4, of $2 ^ 4$ , kan je uitschrijven als 2*2*2*2=16. Vervolgens: “De vierdemachtswortel van 16 is 2”. Dat kan je wiskundig uitschrijven als $\sqrt [4] {16 }$ . Het “omgekeerde” van 4 is 1/4. Je kan wiskundig dus ook schrijven: $\sqrt [4] {16 } = 16 ^ \frac {1}{4}$ . Daarmee kan je in een rekenblad zo’n wortel ook uitrekenen: =16^(1/4) of “zestien tot de macht éénvierde”.
Lang verhaal kort: Worteltrekken is een vorm van machtsverheffen en daarom staat worteltrekken niet in het lijstje.

De instinkertjes

Breuken

$4 \div \frac {2} {4}$ < Een breuk met een tellergetal en een noemergetal wordt als één geheel gezien.
Er staat dus dit: $4 \div \big( \frac {2} {4} \big)$
Of anders geschreven: $4/ ( 2 / 4 )$

Pas dus op met breuken die bestaan uit tellers en noemers.

Dingen zouden ondubbelzinnig moeten zijn maar dat zijn ze niet altijd. Hier volgt nog een breuk met een teller en een noemer:

$\frac {2 a} {4 b}$

Zoiets wordt vaak als tekst in boeken uitgeschreven als $2 a / 4 b$ en dat is dus smeken om problemen. Waarom? Als je daar de regels op loslaat dan komt dit neer op $2 * a / 4 * b$ of $\frac {2*a*b}{4}$ of, korter, $\frac {a * b}{2}$ . Een zekere luiheid om geen haakjes toe te passen kan dus rare resultaten opleveren, zo blijkt.

In het tekstboek had moeten staan: $(2*a)/(4*b)$ of $2*a/(4*b)$ of $a / ( 2 * b )$ .

Merkwaardig genoeg snappen de meeste mensen dat $a * b / 2$ niet bedoeld wordt. Als het in een boek geschreven wordt als $2 a / 4 b$ dan kan het simpelweg verwarrend zijn. Als ik leraar wiskunde was dan zou ik het daarom subiet als fout beoordelen. Immers, $\frac {2 a} {4 b}$ in rekenbladnotatie opschrijven is naar mijn bescheiden mening gewenst: $( 2 * a ) / ( 4 * b )$ of $a / ( 2 * b )$ .

Typografisch gezien is er geen goede reden te bedenken om het niet fatsoenlijk en ondubbelzinnig te schrijven, het lijkt mede een overblijfsel uit tijden met handmatig zetwerk gedurende het drukproces. Er zijn zelfs uitgevers die hier hun eigen regeltjes omheen geschreven hebben.

Goed om te beseffen is dat de manier die gebruikt wordt in rekenbladen ondubbelzinnig is en uiterst efficiënt is. Zie bijvoorbeeld deze bladzijde waar vaak gewisseld wordt tussen $\LaTeX$ en rekenbladnotatie.

Voorbeeld:

$\sqrt [3] { \frac {2} {3} }$ < Wiskundige notatie, levert ~0.874 op.

of…

(2/3)^(1/3) < Rekenbladnotatie, levert eveneens ~0.874 op.

of…

Intermezzo Lisp, BASH…
Programmeertalen vallen en staan bij een juiste syntaxis, de afspraken die we met elkaar maken. Enkele voorbeelden van (2/3)^(1/3):
In Lisp wordt dit geschreven als (expt (/ 2 3) (/ 1 3)) en levert als antwoord 1 op. Dat komt omdat er geen decimale komma gebruikt is en zowel (/ 2 3) als (1/3) de integer 0 oplevert, 0^0 is integer 1. De expressie (expt (/ 2.0 3.0) (/ 1.0 3.0)) levert wel ~0.874 op.
In BASH is de notatie, het commando: let answer=(2/3)**(1/3) waarna echo $$$ answer eveneens 1 oplevert. BASH kan uitsluitend met integers rekenen.

Unaire min-bewerking

Nu we het toch over rekenbladen hebben, nog een instinkertje betreft de unaire bewerking “-“. De volgende som:

$- 3 ^2$ kan op twee manieren opgelost worden:

$- (3^2) = -9$
$(-3)^2 = 9$

De interpretatie is dat het een bewerking of een teken is. Een programma als Excel of LibreOffice Calc ziet het als teken: =-3^2 wordt 9. Echter, in de meeste rekenmachines is het resultaat -9. Als er staat $- 3 ^2$ dan zou je de unaire bewerking minus kunnen zien als een vermenigvuldiging met getal “-1“. Uitgeschreven: $- 3 ^2 = -1*3^2 = -1*9 = -9$

**Rekenblad** (LibreOffice Calc): bewerking -3^2 wordt uitgevoerd als (-3)^2.

**Calculator** (gnome-calculator): bewerking -3^2 wordt uitgevoerd als -(3^2).

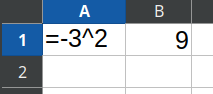
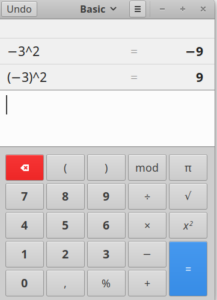
Als dingen niet voor de hand liggend zijn dan doe je er altijd goed aan om haakjes te gebruiken.

Intermezzo: Interpreteert een rekenblad het minus-teken verkeerd?
Strikt genomen interpreteert Microsoft Office Excel (en LibreOffice, LO Calc) het minus-teken niet juist. Immers, formule =-3^2 levert vandaag de dag -9 op en niet 9. Anderzijds was het vroeger wel juist. Rekenbladen worden voor bedrijfskritische processen gebruikt en in de wetenschap. Dus deze bug “herstellen” levert gigantisch veel problemen op met bestaande rekenbladen. Echter, er is ook een goed argument om te stellen dat rekenbladen het wel op de juiste manier doen…
In een rekenblad zijn verwijzingen naar cellen de basis en een cel kan een getalwaarde bevatten. Stel dat cel A1 een waarde van -3 heeft en A2 een formule bevat =A1^2. Het is dan logisch A1 als een reëel getal met waarde -3 te zien en niet als een formule -1*3. Dat is dus een prima reden om het gedrag van rekenbladen te rechtvaardigen. Alternatief: Formule =A1^2 moet je dus eigenlijk lezen als =(A1)^2 – met haakjes, getest in LO Calc.

Tot slot

Al met al is het zo eenvoudig nog niet maar er zijn goede gebruiken en makkelijke ezelsbruggetjes zoals “righty tighty lefty loosey”. Feitelijk zijn de ezelsbruggetjes de standaarden, de normen, om te komen tot de juiste interpretatie.

De kern: Een ander moet altijd goed begrijpen wat je bedoelt. De internet-hype rondom dit onderwerp laat zien dat een heleboel mensen de meest eenvoudige sommetjes totaal verschillend interpreteren.

Daarom: Verduidelijk bij twijfel dingen met haakjes, het is een oplossing voor veel gevallen.