BricsCAD snapt hoe je met geo-coördinaten om moet gaan maar vanilla-AutoCAD? Precies. Hierna volgen stappen die tot een oplossing bijdragen. Afbeeldingen in een CAD-programma invoegen is geen probleem. Als je met de meegeleverde metadata nog iets zinnigs doet dan voorkom je een hoop handmatig gehannes. Wat zijn die metadata? Feitelijk zijn het 6 waarden waarmee de afbeelding precies op de juiste plaats gelegd kan worden. Metadata zitten meestal in een losse zogenaamde “world-file“. In het geval van een GeoTIFF-afbeelding zitten die data in het bestand zelf. Hier wordt verder geen aandacht aan besteedt, focus op de losse world-files. In BricsCAD worden world-files automatisch herkend en verwerkt maar AutoCAD doet dat niet, pindakaas en de reden om hierna wat zaken uit te pluizen.
Table of Contents
Extensies
Dus je hebt een afbeelding lutjebroek.jpg en een bijbehorende world-file lutjebroek.jgw (of lutjebroek.jpgw of lutjebroek.wld), zijnde een tekstbestandje met 6 regels met waarden.
Ieder afbeeldings-bestandsformaat heeft een bijbehorende extensie of de algemene .wld-extensie. Het kan verwarrend zijn, hierbij de mogelijkheden:
- GIF (.gif): .gfw of .gifw of .wld
- JPEG (.jpg): .jgw of .jpgw of .wld
- JPEG 2000 (.jp2): .j2w of .jp2w of .wld
- PNG (.png): .pgw of .pngw of .wld
- TIFF (.tif): .tfw of .tifw of .wld
Lisp
Wat moet een Lisp-programma precies doen? Het antwoord: blader, selecteer een afbeelding, zoek de bijbehorende world-file, lees de parameters, de metadata, verwerk die wiskundig en tot slot moet de afbeelding met de juiste parameters in de tekening terecht komen.
Klinkt simpel maar er komt wel de nodige goniometrie bij kijken en dan hebben we het nog niet gehad over de meeteenheden en natuurlijk het coördinaatsysteem zoals Rijksdriehoek of WGS 84 (GPS) of UTM.
Wat is de betekenis van de regels?
- Regel 1: A: x-component van de pixelbreedte(x-schaal)
- Regel 2: D: y-component van de pixelbreedte (y-skew)
- Regel 3: B: x-component van de pixelhoogte (x-skew)
- Regel 4: E: y-component van de pixelhoogte(y-schaal), meestal negatief
- Regel 5: C: x-coördinaat van het centrum van de pixel linksboven van de originele afbeelding, getransformeerd naar de kaart
- Regel 6: F: y-coördinaat van het centrum van de pixel linksboven van de originele afbeelding, getransformeerd naar de kaart
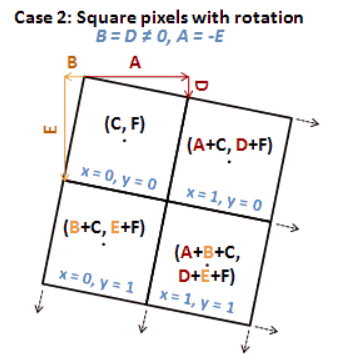
Deze informatie kan je hier verder bestuderen: https://en.wikipedia.org/wiki/World_file .
Coördinaatsystemen
Globaal: Er is WGS 84, UTM en het Rijksdriehoeksysteem (RD). De kans is groot dat een conversie naar RD gewenst is.
Van WGS 84 naar RD bestaan functies, routines, in Lisp die door NedCAD onderhouden worden.
Van UTM naar RD zal via WGS 84 worden uitgevoerd. Er bestaat een bruikbaar algoritme hiervoor: https://en.wikipedia.org/wiki/Universal_Transverse_Mercator_coordinate_system . De uitgelichte afbeelding van deze post is een UTM-kaart waarbij direct opvalt dat Nederland twee UTM-zones heeft, links en rechts van Apeldoorn, ongeveer.
Een eenvoudige case
Er is een world-file en een bitmap…
8×4.png is een bitmap van 8 pixels breed en 4 hoog. Als je browser niet duidelijk de 8 bij 4 blokjes laat zien dan is dat spijtig, maar dit is de afbeelding:


In CAD is er het commando ImageQuality, op 0 in de situatie dat je de pixels wel wil zien.
De inhoud van de world-file 8×4.pgw is als volgt:
1.0
1.0
1.0
-1.0
10
20We gaan uit van RD maar het is een neutraal formaat. In geval van RD komt deze bitmap onder 45 graden ergens bij Parijs uit. Het ziet er als volgt uit, waarbij R1… Regel 1 is, enzovoorts, van 8×4.pgw.
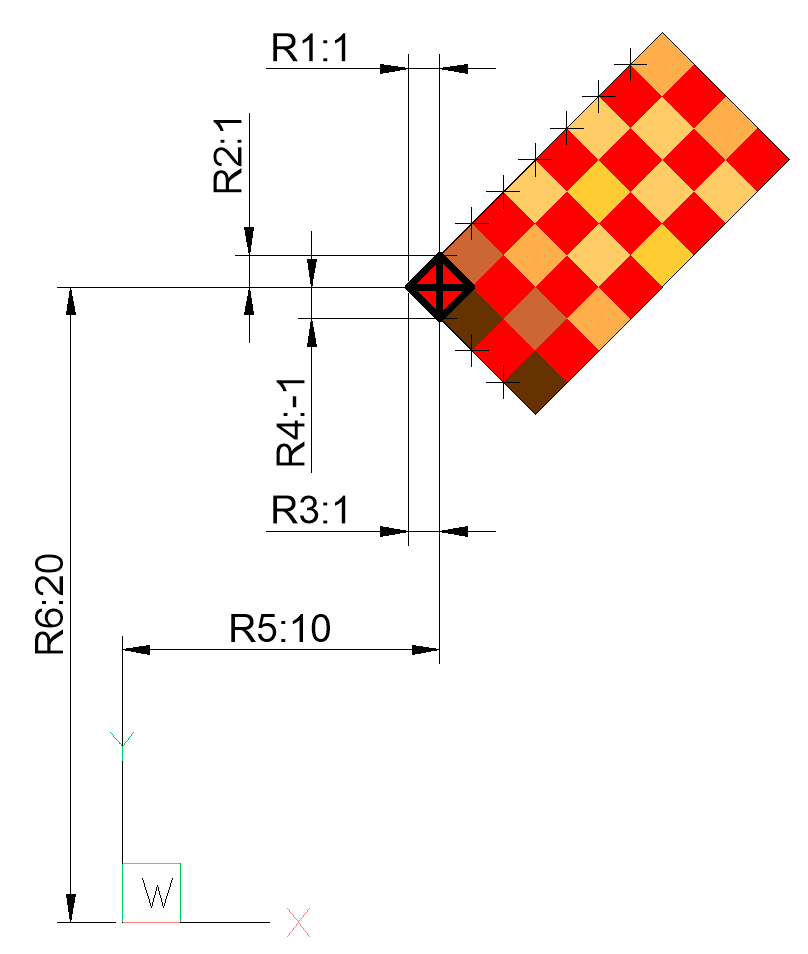
Korte uitleg bij wat je ziet:
- Aan twee zijden van de bitmap is een lijn getekend waar met divide 4 en 8 segmenten gemaakt zijn: de punten die je ziet.
- R1 t/m R4 beschrijven één pixel.
- Cartesiaanse coördinaten: Richting en tekens als in CAD, X horizontaal naar rechts en Y verticaal naar boven.
- R1 en R3 zijn X-waarden van de pixel en R2 en R4 de Y-waarden.
- En dus is R4 negatief
- R5 (X) en R6 (Y) geven de positie aan van het zwaartepunt van de eerste pixel.
Wat conclusies uit onderzoek: Als het aantal dpi in x- en y-richting niet gelijk is in de bitmap dan wordt dat blijkbaar “overruled” door de world-file. Prima!
Tijd om de world-file te veranderen, we maken de y-waarde van de pixel twee keer zo groot, R3 en R4 worden dan resp. 2 en -2. Wat is het resultaat in BricsCAD?
Er wordt een nieuw invoegpunt (Ins.Pt.) berekend. Punt (10,20) loopt door het zwaartepunt van de pixel. Met V22 is een handmatige schaalfactor niet nodig. Het ziet er zo uit.
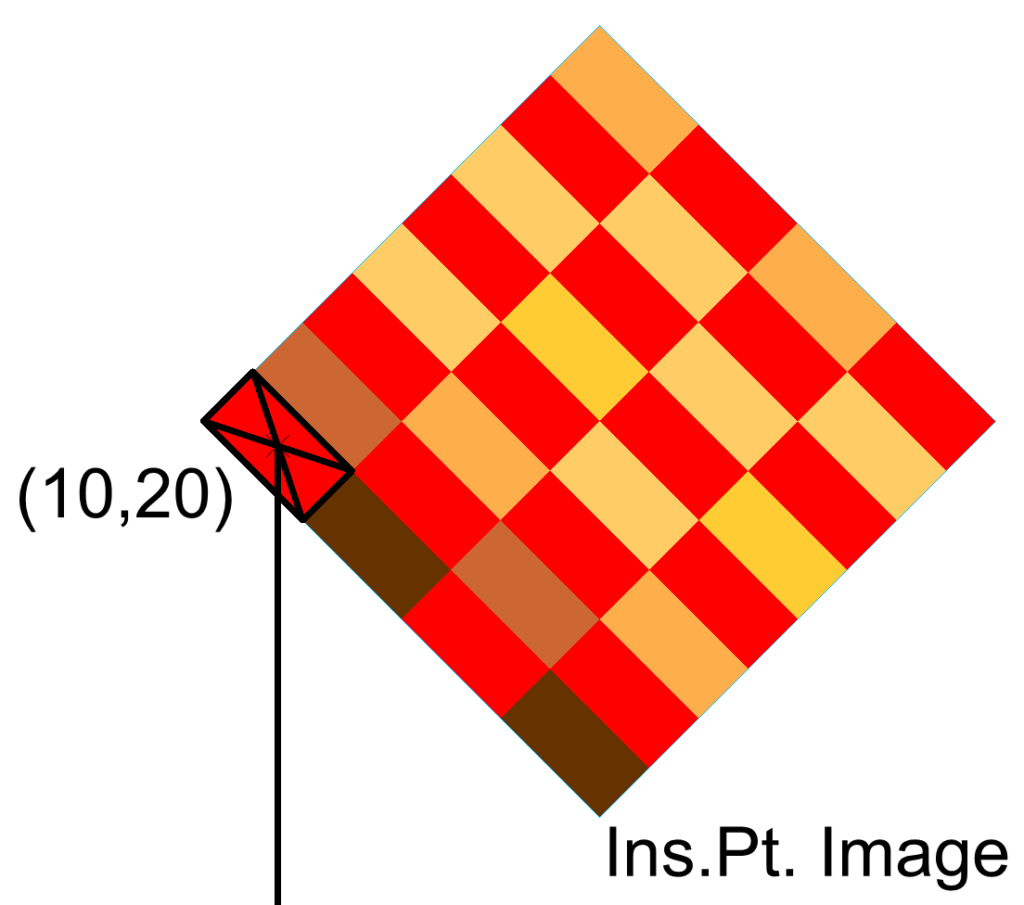
Met andere woorden, de weg voor de juiste schaal is als volgt: Gebruik het invoegpunt uit de world-file, zijnde het zwaartepunt van de eerste pixel links-boven, bereken met de parameters het invoegpunt, de hoek van de bitmap en de hoogte en breedte van een pixel en uiteindelijk de hoogte van de bitmap. Dan resten er opties:
- Als de pixels vierkant zijn dan is er geen probleem.
- Echter, als dat niet zo is dan moet er weer gerekend worden, en…
- In geval van BricsCAD zullen er verschillende x- en y-schalen ontstaan.
- In geval van AutoCAD, die verschillende schalen x- en y-schalen voor bitmaps niet ondersteunt, blijft er maar één hack over waarbij de bitmap omgezet dient te worden tot een block met verschillende schaalfactoren.
- Voorlopige conclusies:
- De automatische geo-positionering in BricsCAD werkt uitstekend en een knop voor commando ImageAttach is er al.
- Voor AutoCAD zal het verder uitgewerkt kunnen worden naar behoefte.
- World-files bevatten pixel-vectoren die niet perse haak staan. CAD-programma’s hebben moeite hiermee, om dit onderwerp niet nog complexer te maken wordt er vanuit gegaan dat de vectoren altijd haaks staan. In code kan altijd een controle uitgevoerd worden.
Een praktijk-case
Er is een world-file met als eerste vier regels:
0.0812001770
0.0118943789
0.0118984182
-0.0812277524Staan die vectoren haaks? Je kan alle volgende code plakken op de commandoregel, onderaan in deze post staat de bron, uit eigen werk:
(if (not acos) (defun acos (r / ) (atan (sqrt (- 1 (expt r 2))) r)))
(defun lv:dot-product (a b / ) (apply '+ (mapcar '(lambda (k l) (* k l)) a b)))
(defun lv:magnitude (a / ) (sqrt (apply '+ (mapcar '(lambda (b) (expt b 2.0)) a))))
(defun lv:vector-ang (a b / ) (acos (/ (lv:dot-product a b) (* (lv:magnitude a) (lv:magnitude b)))))
(setq vector1 (list 0.0812001770 0.0118943789 0.0))
(setq vector2 (list 0.0118984182 -0.0812277524 0.0))AutoCAD kent geen arccosinus-functie, de eerste regel lost dat op. Dan volgen drie functies, voor het inwendig product, de magnitude en de vectorhoek (in radialen). Daarna zijn twee vectoren gedefinieerd, vector1 en vector2.
De eerste vraag, wat is de hoek tussen de vectoren?
(* (/ (lv:vector-ang vector1 vector2) pi) 180)
90.0000000032398 graden. Dat kunnen we bestempelen als haaks. Uiterst belangrijk voor CAD.
De volgende vraag, hoe lang zijn die vectoren, hoe lang zijn de zijden van iedere pixel in x- en y-richting? Makkelijker, we delen die lengtes om een verhouding te krijgen:
(/ (lv:magnitude vector2) (lv:magnitude vector1))1.00033959777363 of makkelijker te doorzien: 3 mm op 10 m is de afwijking. Dat is ook verwaarloosbaar.
Conclusies:
- Een theoretische matrix berekenen en daar “zo goed mogelijk” een bitmap in positioneren is haalbaar.
- “zo goed mogelijk” wil zeggen dat er altijd een afwijking is maar in dit voorbeeld is de projectie 99.99…% zuiver. Het betekent wel dat een programma controles uit moet voeren en aan de bel moet trekken als er onacceptabele afwijkingen ontstaan.
- Het zwaartepunt van de theoretisch matrix valt dan samen met het zwaartepunt van de bitmap en de hoek van de bitmap zal berekend moeten worden op basis van de gewogen gemiddelde hoeken van voorgenoemde vectoren.
Algoritmebepaling
Vele wegen naar Rome. Het algoritme van Bricsys is min of meer bekend en zoveel mogelijk compatibel blijven is handig. Voor het algoritme zijn er randvoorwaarden. R1 is regel 1 van de world-file, enzovoorts…
- Pixels van ingevoegde bitmaps zijn altijd exact vierkant of rechthoekig.
- Voor de breedte van de pixel geldt: breedte =sqrt(r1^2+r2^2).
- De hoogte is daarmee ook bekend indien de pixel vierkant is.
- De hoek van de bitmap wordt gedefinieerd als vector (r1,r2), vector (r3,r4) wordt genegeerd voor dehoekbepaling.
- Voor het bepalen van het zwaartepunt van de eerste pixel geldt:
- Vtl is nu bekend, hoek van de bitmap is de hoek V12, eerder behandeld, let op volgorde argumenten X12 en Y12:
Spreadsheet:=atan2(X12,Y12)*180/pi()
CAD-Lisp:(/ (* 180 (atan Y12 X12)) pi)(lv:r2d (lv:ang2d V1))
- De hoek van V34 is dus hoek V12 – 90 graden, of los berekend:
Spreadsheet:=atan2(Y12,-X12)*180/pi()
CAD-Lisp:-
(/ (* 180 (atan -X12 Y12)) pi) (lv:r2d (lv:ang2d (lv:rot-q3V1)))
-
- Vanaf Vtl de linkeronderhoek van de bitmap bepalen:
- Hoogte van pixel is breedte is lengte V12.
- Pixel-hoogte maal aantal (N) pixels naar beneden:
- V12 is X,Y dus richting is V2-1 of Y,-X.
- Linkeronderpunt Vtl+N*V2-1, uitgeschreven:
X = Xvtl + N * Y12Y = Yvtl + N * -X12
- Dat is alles voor vierkante pixels. Echter, als pixels rechthoekig zijn, dan zijn er enkele aannamen:
- V34 staat -90 graden t.o.v. V12, i.p.v. dat we de hoek van de vector V34 zelf berekenen, zoals hiervoor ook bewust gedaan op basis van V12.
- De breedte van een pixel:
Bp = sqrt (X12^2 + Y12^2) - De hoogte van een pixel:
Hp = sqrt (X34^2 + Y34^2)
- Voor Vbl (bottom left) is de berekening hetzelfde als bij vierkante pixels met als aanvulling dat er vermenigvuldigd moet worden met uiteraard een factor Hp/Bp, zie hierna.
Samenvatting berekening
Kunnen we dan alles op één hoop gooien? Jazeker! Een samenvatting, gegeven een world-file:
X12
Y12
X34
Y34
X56
Y56
Case: vierkante pixels
V34, dus X34 en Y34, worden niet gebruikt.
- De linker-bovenpunt van de bitmap, Vtl = (Xtl,Ytl):
Xtl = X56 + (X12 + Y12) / -2
Ytl = Y56 + (Y12 - X12) / -2 - De linker-onderpunt van de bitmap, bij een hoogte van N pixels, Vbl = (Xbl,Ybl):
Xbl = X56 + (X12 + Y12) / -2 + N * Y12
Ybl = Y56 + (Y12 - X12) / -2 + N * -X12
Case: rechthoekige pixels
- De linker-bovenpunt van de bitmap, Vtl = (Xtl,Ytl):
Xtl = X56 + (X12 + X34) / -2Ytl = Y56 + (Y12 + Y34) / -2 - De linker-onderpunt van de bitmap, bij een hoogte van N pixels, Vbl = (Xbl,Ybl):
Xbl = X56 + (X12 + X34) / -2 + N * Y12 * Hp / Bp
Ybl = Y56 + (Y12 + Y34) / -2 + N * -X12 * Hp / Bp
Algemene oplossing Lisp
We gaan uit van rechthoekige pixels, dat dekt immers ook de oplossing met vierkante pixels. Je hebt de variabelen allemaal toegekend. We moeten dan wel uitgaan van coördinaten die haaks staan. We lenen wat functies van lib-vector, je kan die kopieren en laden. Dit is de code:
;Setting variables (setq X12 3.0 Y12 2.0 X34 3.0 Y34 -4.5 X56 8.0 Y56 20.0 ; X Y coordinates N 4 M 6 ; Bitmap size V1 (list X12 Y12) V2 (list X34 Y34) V3 (list X56 Y56) ; Vectors ) ; Vofs... (setq Vofs (lv:divide (lv:add V1 V2) -2.0)) ; Vtl... (setq Vtl (lv:add V3 Vofs)) ; Vtl on one line... (setq Vtl (lv:add V3 (lv:divide (lv:add V1 V2) -2.0))) ; Angle of bitmap dir. V1... (lv:ang2d V1) ; radians (lv:r2d (lv:ang2d V1)) ; degrees ; Angle of bitmap dir. V2... (lv:ang2d (lv:rot-q3 V1)) ; radians (lv:r2d (lv:ang2d (lv:rot-q3 V1))) ; degrees ; Ratio pixel height/width... (/ (lv:magnitude V2) (lv:magnitude V1)) ; Vbl (setq Vbl (lv:add Vtl (lv:multiply (lv:multiply (lv:rot-q3 V1) (/ (lv:magnitude V2) (lv:magnitude V1))) n))) |
+++++
(courtesy featured image…)