Skip to content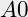 is een formaat van precies
is een formaat van precies 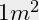 met de verhouding van de zijden
met de verhouding van de zijden
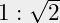
(de wortel van 2 is ongeveer 1,41).- Knip je een
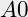 in tweeën – start aan de langste zijde – dan blijft de verhouding van de zijden
in tweeën – start aan de langste zijde – dan blijft de verhouding van de zijden 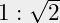 , ook als je dat daarna weer in tweeën knipt.
, ook als je dat daarna weer in tweeën knipt.- Die helft van
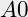 is
is 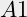 , de helft van
, de helft van 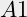 is
is 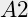 , idem
, idem 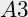 en
en 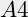 .
.
Een 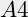 is dus
is dus
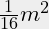 .
.
- “80 grams papier” wil zeggen dat één vierkante meter 80 gram weegt.
- Een “80 grams A4-tje” weegt dus
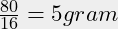
en dat is handig voor het berekenen welke postzegel nodig is. - Als grove vuistregel: Een 80 grams vel is ongeveer 0.1 mm dik. Een boek van 1 cm dik telt dus ongeveer 100 bladen, dus 200 bladzijden. Voor kopieerpapier klopt dit redelijk en het is afhankelijk van de “opdikking” van het papier in kubieke centimeters per gram
- Als een
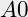 een oppervlak heeft van
een oppervlak heeft van 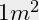 , met zijden
, met zijden 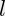 en
en 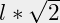 , hoe groot zijn dan de zijden? Oppervlak:
, hoe groot zijn dan de zijden? Oppervlak:
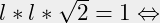
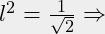
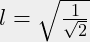
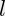 is de korte zijde, de lange zijde is dus:
is de korte zijde, de lange zijde is dus:

ofwel “ongeveer”: 0,840896415253715 bij 1,18920711500272 meter.
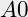 is een formaat van precies
is een formaat van precies 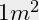 met de verhouding van de zijden
met de verhouding van de zijden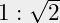
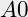 in tweeën – start aan de langste zijde – dan blijft de verhouding van de zijden
in tweeën – start aan de langste zijde – dan blijft de verhouding van de zijden 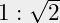 , ook als je dat daarna weer in tweeën knipt.
, ook als je dat daarna weer in tweeën knipt.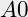 is
is 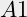 , de helft van
, de helft van 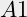 is
is 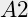 , idem
, idem 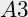 en
en 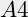 .
.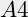 is dus
is dus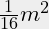 .
.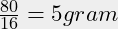
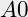 een oppervlak heeft van
een oppervlak heeft van 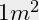 , met zijden
, met zijden 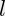 en
en 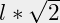 , hoe groot zijn dan de zijden? Oppervlak:
, hoe groot zijn dan de zijden? Oppervlak: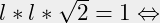
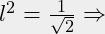
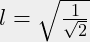
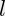 is de korte zijde, de lange zijde is dus:
is de korte zijde, de lange zijde is dus:
Het gramsgewicht alleen zegt lang niet alles over de dikte van papier. Veel papiersoorten zijn “gestreken”, wat meestal betekent dat er een dunne kleicoating overheen zit; die coating weegt ook mee en is relatief zwaar. En het oppervlakte van papier kan vlak of minder vlak zijn, dat kan ervoor zorgen dat een stapel dikker is dan je zou verwachten (“opdikking”: de verhouding tussen dikte en gramgewicht).
Bedankt voor je reactie Jan, de tekst is wat aangepast. Grappig om te zien dat de papierindustrie dus eigenlijk de omgekeerde soortelijke massa gebruikt voor “opdikking”.